Содержание
NP класс и NP-полные задачи
Вопросы и ответы про $NP, P$ и т.д.
Что такое класс $P$?
$P$ – класс задач, решаемых за полиномиальное (от размера входа) время. Примеры таких задач: задача о существовании пути в графе, задача о взаимно простых числах и т.д.
Что такое полиномиальное время?
Говорят, что алгоритм работает за полиномиальное время, если время работы ограничено сверху многочленом от размера входа алгоритма, то есть $T(n)=O(n^k)$ для некоторой константы $k$.
(Примерами задач являются целочисленное сложение, умножение, деление, взятие остатка от деления, умножения матриц, выяснение связности графов, сортировка множества из $n$ чисел, нахождение эйлерова цикла на графе из $m$ рёбер, обнаружение в тексте длиной $n$ некоторого слова, построение покрывающего дерева минимальной стоимости)
Что такое класс $NP$?
$NP$ – класс задач, верифицируемых (проверяемых) за полиномиальное время. Альтернативное определение: класс задач, решаемых за полиномиальное время на недетерминированной машине Тьюринга. Примеры таких задач: задача о выполнимости булевой формулы, задача о вершинном покрытии, задача о клике и т.д.
Как доказать, что задача принадлежит классу $NP$?
Существует два варианта:
- Привести алгоритм решения задачи, работающий полиномиальное время на недетерминированной машине Тьюринга.
- Описать сертификат и привести алгоритм верификации, работающий полиномиальное время на детерминированной машине Тьюринга.
Сертификат – дополнительная информация, позволяющая быстро решить задачу. Важно помнить, что размер сертификата должен быть полиномиален относительно размера самой задачи.
Алгоритм верификации – принимает на вход экземпляр задачи и сертификат к нему, а возвращает ответ к задаче, 0 или 1.
Какие задачи называются $NP$-трудными?
Это задачи, к которым сводимы все задачи из класса $NP$ за полиномиальное время. При этом не требуется, чтобы сама задача принадлежала классу $NP$, она может быть более сложной.
Что значит, что одна задача водима к другой за полиноминальное время?
Это значит, что существует полиномиальная функция, которая отображает экземпляр первой задачи в экземпляр второй задачи. Если входная задача соответствует положительному решению, то и выходная задача соответствует положительному решению. Если входная задача соответствует отрицательному решению, то и решение выходной задачи отрицательно.
Какие подходы к решению $NP$-трудных задач?
- Полный перебор (Brute force)
- Приближенное решение (с оценкой точности и с вероятностью ошибки)
- Стремление к полиномиальному решению в среднем (в худшем случае задача остается нерешаемой за полиномиальное время)
Какие задачи называются $NP$-полными?
$NP$-трудные задачи, принадлежащие классу $NP$.
Примеры: 3Sat, задача о вершинном покрытии (множество вершин, такое, что, у каждого ребра графа хотя бы один из концов входит в вершину из него) и т.д.
Как доказать, что задача является $NP$-трудной?
Существует два варианта:
- (Практически никогда не используется) Доказать, что все задачи из класса $NP$ сводится к данной. Таким способом была определена первая $NP$-трудная (и -полная) задача – Sat.
- (Основной) Доказать, что к данной задаче сводится (за полиномиальное время) какая-нибудь $NP$-трудная задача. Отсюда следует, что все задачи можно свести к данной, так как любую задачу из $NP$ можно свести к $NP$-трудной задаче, а ее в свою очередь к данной.
Как доказать, что задача является $NP$-полной?
- Доказать, что она $NP$-трудная.
- Доказать, что она принадлежит $NP$.
Общая схема и проблема $NP=P$
Гипотеза $NP=P$
Существует гипотеза $P=NP$ (одна из центральных проблем теории алгоритмов). Гипотеза гласит, что если решение задачи можно быстро проверить, то саму задачу можно быстро решить. Гипотезу не могут ни опровергнуть, ни доказать уже более 30 лет.
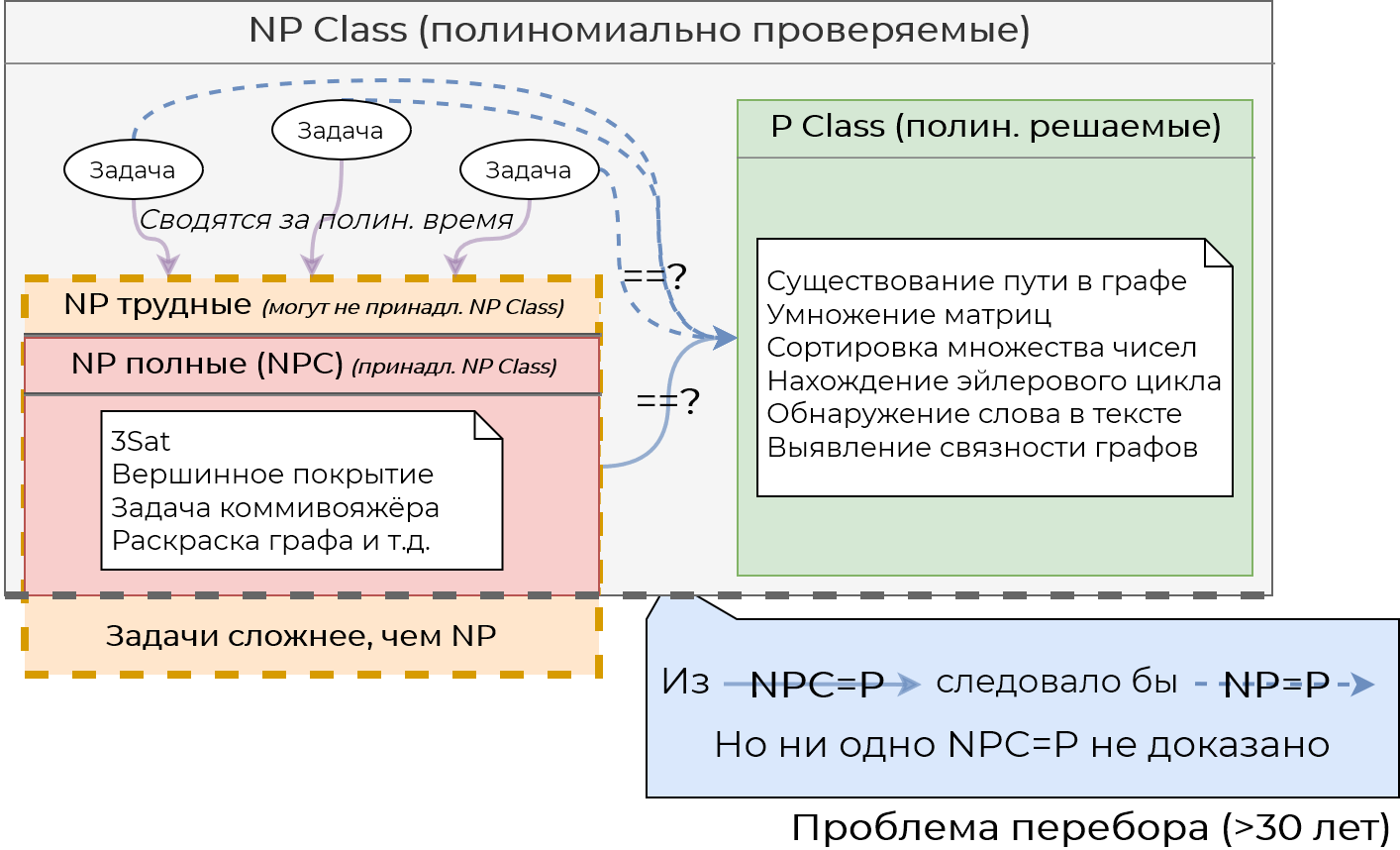
Общая схема классов
Обратим внимание на знаки ==? на рисунке. Если хотя бы одна $NP$-полная (иначе говоря NPC) задача будет принадлежать классу $P$, то все остальные задачи из класса $NP$ также будут принадлежать классу $P$. Говоря на «языке рисунка»: из синей стрелки следуют синие пунктирные стрелки. Именно так должно доказываться равенство $NP=P$.
Но тем не менее, ни одной $NP$-полной задачи, которая принадлежала бы классу $P$, не было найдено.