Дополним обычную задачу поиска подстроки в тексте необходимостью найти вхождения k подстрок. Нам известны алгоритмы, производящие поиск для одной подстроки, длина которой не превосходит длины текста за O(n), где n – длина текста. Таким образом, если пользоваться этими алгоритмами, то для k подстрок нам придётся выполнить k процедур поиска, что приведёт к результирующей сложности в O(nk), что не очень-то и эффективно. Для решения этой проблемы существует алгоритм Ахо-Корасик.

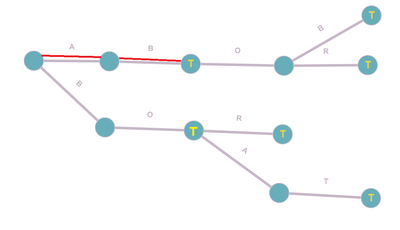
Искомые подстроки мы будем хранить в боре. Бор - это корневое дерево, каждому ребру которого соответствует определённый символ. Каждая вершина дерева содержит в себе пометку о том, является ли она терминальной, то есть заканчивается ли на ней входящая в бор строка. Таким образом, строка, хранящаяся в боре, представляется как путь от корня до терминальной вершины. Так, например на нижеприведённой иллюстрации, слову «AB» будет соответствовать путь, выделенный красным.

Пример реализации структур данных бора на языке Python:

class Node:
    def __init__(self, value, parent):
        self.value = value
        self.is_end = False
        self.children = {}
        self.parent = parent
 
    def add_child(self, value, node):
        self.children[value] = node
 
    def set_end(self):
        self.is_end = True
 
    def get_way(self):
        node = self
        sttr = ""
        while node.value != None:
            sttr = node.value + sttr
            node = node.parent
        return sttr
 
 
 
class Trie:
    def __init__(self):
        self.root = Node(None, None)
        self.root.parent = self.root
 
    def add_word(self, word):
        node = self.root
        for letter in word:
            if letter not in node.children:
                new_node = Node(letter, node)
                node.add_child(letter, new_node)
            node = node.children[letter]
        node.set_end()

Код 1. Основные структуры данных бора

С данными структурами данных, мы уже можем реализовать алгоритм поиска вхождений всех искомых подстрок полным перебором, который будет начиная с каждой позиции в тексте будет проверять вхождение начинающейся с неё подстроки в бор, и на каждом посещении терминальной вершины будет добавлять найденную строку в выходной массив.

def Bruteforce_Search(text, patterns):
    trie = Trie()
    answer = []
    for word in patterns:
        trie.add_word(word)
    for i in range(len(text)):
        current_state = trie.root
        for letter in text[i:]:
            if letter not in current_state.children:
                break
            else:
                current_state = current_state.children[letter]
                if current_state.is_end:
                    answer.append((i, patterns.index(current_state.get_way())))
    return answer

Код 2. Алгоритм поиска полным перебором.

Приведённый алгоритм выдаёт список кортежей длины 2, где на первой позиции находится индекс, с которого начинается найденный шаблон и индекс шаблона в передаваемом в функцию списке шаблонов.

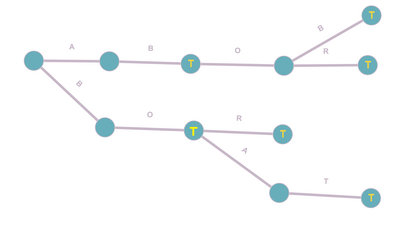
Можно заметить, что как только алгоритм встречает символ, по которому отсутствует переход в боре, он переходит к следующему начальному элементу. При этом можно заметить, что в боре могут содержаться некоторые суффиксы текущей строки. Так, например, в уже построенном нами боре

для строки ABO содержится также суффикс BO, по которому было бы выгодно перейти, например при поиске по строке ABOAT. Таким образом мы пришли к идее построения суффиксных ссылок, по которым алгоритм поиска переходил бы при встрече «плохого» символа, т.е. по которому нельзя пройти дальше по бору. Также заметим, что нам достаточно хранить суффиксную ссылку только на самый длинный суффикс, так как второй по длине суффикс будет самым длинным суффиксом первого и т.д., то есть проходя по цепочке суффиксных ссылок можно попасть в каждый суффикс, имеющийся в дереве. Также заметим, что суффикс должен быть короче исходной строки, и может быть нулевой строкой (тогда суффиксная ссылка будет вести в корень бора). Переход по такой ссылке будет обозначать, что мы начали обход бора заново. Так как у нулевой строки нет суффиксов, то суффиксная ссылка для корня может быть NULL/None или указывать на сам корень. Последний подход считается наиболее удобным. Для построения суффиксных ссылок можно заметить, что для вершины v, суффиксная ссылка её дочерней вершины по символу с будет вести на дочернюю вершину по символу с одной из суффиксных ссылок вершины v (или на корень, в случае если ни одна из суффиксных ссылок по цепочке не имеет детей по символу с). Таким образом для построения суффиксных ссылок было бы полезно иметь уже построенные суффиксные ссылки для родителя текущей вершины. Учитывая, что длина строки для родительской вершины и для суффиксных ссылок всегда меньше длины строки для текущей вершины, можно воспользоваться алгоритмом обхода в ширину (BFS). Этот алгоритм обходит вершины так, что для всех строк, более коротких чем текущая суффиксные ссылки будут гарантировано просчитаны.

class Node:
    def __init__(self, value, parent):
        self.value = value
        self.is_end = False
        self.children = {}
        self.suffix_link = None
        self.parent = parent
 
 
class Trie:
    def __init__(self):
        self.root = Node(None, None)
        self.root.parent = self.root
        self.root.suffix_link = self.root
 
    def gen_suffix_links(self):
        queue = [self.root]
        while queue:
            node = queue.pop(0)
            for child in node.children.values():
                queue.append(child)
            parent = node.parent
            while parent is not parent.suffix_link:
                if node.value in parent.suffix_link.children:
                    node.suffix_link = parent.suffix_link.children[node.value]
                    break
                parent = parent.suffix_link
            else:
                node.suffix_link = self.root

Код 3. Генерация суффиксных ссылок (приведены только модифицированные функции)

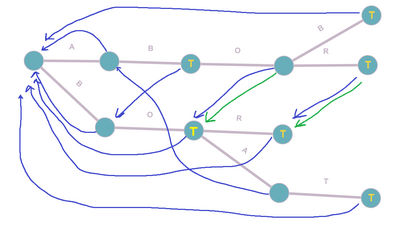
Можно заметить, что для случая, когда в дереве будет только одна строка, суффиксные ссылки будут соответствовать префикс-функции, используемой в алгоритме Кнута-Морриса-Пратта. Построим суффиксные ссылки для нашего бора из примера:

Давайте предположим, что мы ищем строки, представленные в нашем боре в строке ABORAB. Проходя по бору, мы приходим в вершину ABOR. Мы уже нашли строки AB и ABOR. В боре нет вершины, соответствующей строке ABORA, так что переходим по суффиксной ссылке в BOR. BOR – терминальная вершина, добавляем её в массив ответов. Так как BORA также отсутствует в боре, переходим по суффиксной ссылке в корень, оттуда на A. Оттуда уже переходим в B и находим вхождение AB. Строка завершается, и алгоритм завершается. Таким образом мы потеряли вхождение строки BO. Для предотвращения таких потерь можно на каждой итерации проходить по всем суффиксным ссылкам, проверяя каждую ссылку на терминальность, но это вызовет ненужный рост временной сложности. Вместо этого можно добавить ещё один тип ссылок – терминальные ссылки, то есть ссылки, ссылающиеся на самый длинный суффикс, являющийся строкой из искомого набора. Построение таких ссылок можно производить одновременно с построением обычных суффиксных ссылок, просто проверяя является ли построенная суффиксная ссылка терминалом. В случае, если является – терминальная ссылка равняется суффиксной, иначе – терминальная ссылка становится равна терминальной ссылке найденного суффикса. Таким образом при обходе вершины при наличии терминальных ссылок мы сможем пройти по их цепочке и обозначить найденные подстроки, при этом не проходя по заведомо не терминальным вершинам. Добавим построение терминальных ссылок к уже имеющемуся коду.

class Node:
    def __init__(self, value, parent):
        self.value = value
        self.is_end = False
        self.children = {}
        self.suffix_link = None
        self.terminal_link = None
        self.parent = parent
 
class Trie:
    def gen_suffix_links(self):
        queue = [self.root]
        while queue:
            node = queue.pop(0)
            for child in node.children.values():
                queue.append(child)
            parent = node.parent
            while parent is not parent.suffix_link:
                if node.value in parent.suffix_link.children:
                    node.suffix_link = parent.suffix_link.children[node.value]
                    break
                parent = parent.suffix_link
            else:
                node.suffix_link = self.root
            if node.suffix_link.is_end:
                node.terminal_link = node.suffix_link
            else:
                node.terminal_link = node.suffix_link.terminal_link

Код 4. Генерация суффиксных и терминальных ссылок (приведены только модифицированные функции)

Покажем терминальные ссылки для нашего бора:

Теперь осталось лишь реализовать вышеизложенные идеи, реализовав необходимые проходы по ссылкам.

def AhoCorasick(text, patterns):
    trie = Trie()
    output = {}
    for pattern in patterns:
        trie.add_word(pattern)
        output[pattern] = []
    trie.gen_suffix_links()
    state = trie.root
    for i in range(len(text)):
        if text[i] in state.children:
            state = state.children[text[i]]
        else:
            while text[i] not in state.children and state != trie.root:
                state = state.suffix_link
            if text[i] in state.children:
                state = state.children[text[i]]
        if i == 6:
            pass
        statecp = state
        if statecp.is_end:
            output[statecp.get_way()].append( i - len(statecp.get_way()) + 1)
        while statecp.terminal_link is not None:
            statecp = statecp.terminal_link
            output[statecp.get_way()].append( i - len(statecp.get_way()) + 1)
    return output

Код 5. Реализация алгоритма Ахо-Корасик

Приведённая реализация на языке Python принимает текст и список искомых шаблонов, и возвращает словарь, где ключами являются искомые подстроки, а значениями – списки позиций, с которых начинаются их вхождения в текст.

1. Alfred V. Aho, Margaret J. Corasick. Efficient string matching: An aid to bibliographic search Communications of the ACM. — 1975. — Т. 18, № 6. — С. 333—340. — doi:10.1145/360825.360855. 2. Алгоритм Ахо-Корасик https://web.archive.org/web/20240131031632/https://e-maxx.ru/algo/aho_corasick